Spring and Dampener System Design for Lunar Excursion Module
Introduction:
The purpose of this project is to design a spring and a dampener for the system in order to obtain a specified period of vibration. The engineers will use their knowledge of mechanical vibration, physics, and mechanical systems to begin solving the problem. The design will encompass a range of values for spring rate and a dampener that we receive from a MATLAB script written to gather this information.
Problem Statement:
The lunar excursion module (see figure below) has been modeled as a mass supported by four symmetrically located legs, each of which can be approximated as a spring-damper system with negligible mass. Design the springs and dampers of the system in order to have the damped period of vibration between 1 and 2 seconds.
Figure 1: Lunar excursion module

Mathematical Formulation:


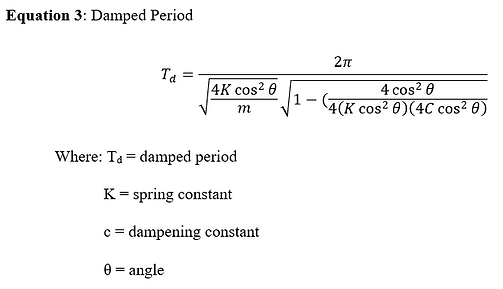

Analysis/Solution:
Solving for spring constant based on an initial guess of c=20,000 N-s/m
Figure 2: Matlab script to determine a range of spring constants
Looking up online for typical values of damping constants, a value of 20,000N-s/m was found for one particular automotive vehicle. The reason an automotive vehicle was used as a reference point was that the weight is similar to that of a large vehicle. Due to having an unknown damping constant and spring constant, a MATLAB script was written to use a damping constant of 20,000N-s/m and find a range of spring constant values that would allow for a damped period between 1 to 2 seconds.
Solving for damping factor based on an initial guess of K=48,000 N/m

Figure 3: Matlab script to determine a range of dampening constant
When looking online for typical values of spring constants, a value of 50,000N/m was found. The MATLAB script was changed so that a spring constant value of 50,000N/m was used to determine the range of damping constant values that would keep the damped period within 1 to 2 seconds. Looking at the commented out lines in Figure 2 and Figure 3, one can see the range of values per input. In addition, different scenarios were listed out in lines 17, 18, and 19. The damping constant and spring constant indicated in the code is the equivalent damping constant and equivalent spring constant, respectively. Therefore, by dividing four, the individual damping constant and individual spring constant can be determined for each leg.
Conclusion:
For the lunar excursion module, a damped period of vibration was desired to be between 1 and 2 seconds. The damped period equation (Equation 3) was useful but there were two unknowns. By doing some research on vehicles, a typical damping constant was around 20,000Ns/m and a typical spring constant was around 50,000N/m. MATLAB was used to plug in one of the constraints and solve for a range that works for the other constraint. The spring constant was given more priority and some final combinations are shown in Table 1.

